R 다변량 통계 분석 - 4. 다변량 정규성 검정, 상관계수, 직선성, 주성분 분석, 주성분 정규성, correlation, qqplot, Principal component analysis, PCA, screeplot, biplot

아래 내용은 <R과 함께하는 다변량 자료분석을 위한 추정과 검정, 최용석 지음, 2019>에서 대부분 발췌하였습니다

R과 함께하는 다변량 자료분석을 위한 추정과 검정, 최용석 지음, 2019

다변량 통계 분석에서 정규성 검정, 시각화 방법 등에 필요한 라이브러리 입니다

 

library(MVT)
library(MVN)
library(dplyr)
library(car)
library(multifluo)

library(chemometrics)

library(DMwR)

library(tidyr)
library(data.table)
library(corrplot)
library(factoextra)
library(FactoMineR)

 

 

#### Q-Q plot의 직선성을 상관계수로 검토하라

### 일변량 데이터 상관계수

일변량 데이터는 cor()함수와 qqnorm()함수로 상관계수를 구하여 직선성을 구할 수 있습니다

실습에 사용할 데이터를 불러오겠습니다

klpga.txt

0.00MB

klpga <- read.table("D:/klpga.txt", header = TRUE)  klpga <- klpga %>% data.frame()

 

그린적중율 변수만 상관계수를 구하여 직선성을 구해보겠습니다

그린 <- klpga %>% select(그린적중율) 그린_vector <- 그린 %>% as.vector() 그린_vector <- 그린_vector %>% unlist() 그린_num <- 그린_vector %>% as.numeric() 그린_norm <- qqnorm(그린_num, pch = 1, main = "Q-Q plot(2)-green") qqline(그린_num, col = "Blue", lwd = 2) 그린_sort_norm_x <- 그린_norm$x %>% sort() 그린_sort_norm_y <- 그린_norm$y %>% sort() cor(그린_sort_norm_x, 그린_sort_norm_y)

#plot

# correlation(상관계수)

실제 데이터가 아니지만 0.983정도면 굉장히 높은 수치입니다

그만큼 직선(qqline)에 관측치가 잘 모여있다고 할 수 있습니다

 

 

### 다변량 데이터 상관계수

klpga 데이터를 살펴보겠습니다
기술요인변수와 경기성적요인변수로 구성되어있습니다

변수명	요인
평균퍼팅수	경기성적요인
그린적중율	기술요인
파세이브율	기술요인
파브레이크율	기술요인
평균타수	경기성적요인
상금율	기술요인

 

요인별로 변수를 분리해보겠습니다

기술 <- klpga %>% select(그린적중율,파세이브율,파브레이크율,상금율) 경기성적 <- klpga %>% select(평균퍼팅수, 평균타수)

 

기술 data.frame만 다변량 상관계수를 구해보겠습니다

기술_n <- 기술 %>% nrow() 기술_p <- 기술 %>% ncol() 기술_s <- 기술 %>% cov() 기술_bar <- 기술 %>% colMeans() 기술_m <- mahalanobis(기술, 기술_bar, 기술_s) 기술_m <- 기술_m %>% sort() 기술_id <- seq(1,기술_n) 기술_pt <- (기술_id-0.5)/기술_n 기술_q <- qchisq(기술_pt,기술_p) 기술_rq <- cor(기술_q, 기술_m)

다변량 상관계수는 0.9325682입니다

 

 

 

#### 주성분 분석을 활용한 시각적 방법과 검정방법에서 설명력이 높은 두 성분을 활용하여 다변량 정규성을 검토

### 주성분 분석 활용 

작업을 위해 추가적으로 필요한 라이브러리는 다음과 같습니다

library(tidyr)
library(data.table)
library(corrplot)
library(factoextra)
library(FactoMineR)

 

# 상관계수

데이터 전체를 파악할 겸 변수간 상관계수를 구해봅시다

klpga_cor <- klpga %>% cor()

 

흐름을 좀 더 직관적으로 파악하기 위해 시각화 해봅시다

klpga_corr <- klpga_cor %>% corrplot()

기술요인과 경기성적요인은 반대로 움직인다는 것을 확인 할 수 있었습니다

 

 

### 주성분 분석

변수간의 상호 움직임을 확인했으면 다변량 통계분석의 핵심중 하나인 주성분 분석에 대해 알아봅시다

https://ko.wikipedia.org/wiki/%EC%A3%BC%EC%84%B1%EB%B6%84_%EB%B6%84%EC%84%9D

주성분 분석 - 위키백과, 우리 모두의 백과사전

주성분 분석(Principal component analysis : PCA)은 여려 변수들로 이루어진 다차원의 데이터를 축소하는 기법입니다
주성분 분석은 데이터를 한개의 축으로 사상시켰을 때 그 분산이 가장 커지는 축을 첫 번째 주성분, 두 번째로 커지는 축을 두 번째 주성분으로 놓이도록 새로운 좌표계로 데이터를 선형 변환합니다

 

구하는 방법은 복잡하기도 하고 워낙 많은 개념을 이해해야 되서 자세한 설명은 넘어가도록 하겠습니다

여러 수리통계적 이론이 들어가지만 실제로 손으로 구하는 분은 한번도 본적 없기도 하고...

우리는 결과를 해석하는 것 위주로 정리 하겠습니다

 

※ 주성분 분석과 가장 많이 혼동하는 것이 요인분석(factor analysis)입니다 차원을 축소한다는 공통점이 있는지라 서로간의 관계가 명확하지 않은 느낌이 있습니다. 다만 주성분 분석은 축소한 주성분 간에는 반드시 독립적이어야 하지만(직교회전) 요인분석은 그렇지 않습니다. 자세한 차이점은 다른 문헌을 참조해주시기 바랍니다

 

 

## 주성분 분석 실행하기

주성분 분석을 해보겠습니다

간략한 정보를 보기위해 summary() 함수도 사용하겠습니다

klpga_pca <- klpga %>% PCA(graph = FALSE)  klpga_pca %>% summary()

결과값이 나옵니다 이것만 가지고는 해석이 한눈에 들어오지 않을수 있기에

추가적으로 코드를 실행해보겠습니다

 

 

## 주성분(comp) 파악하기

앞서 언급하였지만, 주성분 분석은 데이터를 한개의 축으로 사상시켰을 때 그 분산이 가장 커지는 축을 첫 번째 주성분, 두 번째로 커지는 축을 두 번째 주성분으로 놓이도록 새로운 좌표계로 데이터를 선형 변환합니다

 

그럼 첫 번째 주성분, 두 번째 주성분을 파악해보겠습니다

klpga_pca_comp <- klpga_pca$eig klpga_pca_comp %>% View()

결과값을 해석해봅시다

우선 eigenvalue가 무엇인지 알아보겠습니다(많이 깁니다)

 

 

 

# 고유값(eigenvalue) 고유벡터(eigenvector)

우선 벡터(vector)에 대해 잠깐 짚고 넘어가겠습니다 

벡터는 크기만을 가지는 스칼라(scalar)와 방향(direction) 구성되어있습니다

 

그러면 고유값(eigenvalue) 고유벡터(eigenvector)는 무엇이며, eigen(고유)는 왜 쓰는 것일까요

수학적 정의를 집고 넘어갑시다

Ax=λx λ가 실수 공간에 속할때(λ∈R), 정방행렬(square matrix) A의 고유벡터(eigenvector)는 영벡터가 아닌 벡터(nonzero vector) x이다. 또한, λ는 A의 고유값(eigenvalue)이다

이게 무슨 말일까요?

이 정의를 이해하거나 계산하기 위해서는 선형대수학적 지식이 필요하기에 수리적 설명은 하지않겠습니다

 

 

여기서 다시 한번 주성분 분석이 무엇인지 보겠습니다(슬슬 질리겠지만...)

주성분 분석은 데이터를 한개의 축으로 사상시켰을 때 그 분산이 가장 커지는 축을 첫 번째 주성분, 두 번째로 커지는 축을 두 번째 주성분으로 놓이도록 새로운 좌표계로 데이터를 선형 변환합니다

여기서 주목해야하는 단어는 선형 변환입니다

차원 축소를 위해서든 다른 목적이든 벡터를 좌표평면(x축, y축) 상에서 확대, 축소, 회전하는 행위를 변환이라고 합니다

선형 변환은 벡터를 선형(linear)으로 변환하는 것이라 할 수 있습니다

(정확한 수리적 정의와는 다소 차이가 있습니다만, 이렇게 이해하셔도 무방합니다)

 

그 선형 변환을 위해 필요한 것이 고유값(eigenvalue) 고유벡터(eigenvector)입니다

eigen-은 무엇을 뜻하는지 번역기를 써보겠습니다

저는 eigen- 영단어 번역중 particular가 가장 이해가 잘되었습니다

particular 형용사로 쓰일때 1. 특정한 2. 특별한 3. 까다로운 뜻을 가지고 있습니다

 

어떤 점이 특별할까요?

고유벡터(eigenvector)는 일반적인 벡터와 달리

방향(direction)은 바뀌지 않은채, 좌표평면 위에서 크기(scalar)만 바뀌는 성질이 특별(eigen)합니다 

고유값(eigenvalue)는 고유벡터가 특별한 성질로 방향은 바뀌지 않고 크기만 바뀔때 크기가 고유값입니다

 

고유값(eigenvalue) 고유벡터(eigenvector)는 다변량 통계분석 뿐만 아니라 선형모형(Linear Model) 같은 기초과목 뿐만 아니라 데이터마이닝, 머신러닝 등 가장 트렌디한 분야에서도 반드시 접하는 개념입니다

매우 중요한 개념이니 최종정리를 합시다

Ax=λx λ가 실수 공간에 속할때(λ∈R), 정방행렬(square matrix) A의 고유벡터(eigenvector)는 영벡터가 아닌 벡터(nonzero vector) x이다. 또한, λ는 A의 고유값(eigenvalue)이다   고유벡터(eigenvector)는 임의의 벡터를 선형변환 했을때 방향은 고정된 채 크기만 변하는 벡터입니다 고유값(eigenvalue)는 임의의 벡터를 선형변환 했을때 변환된 크기입니다

 

다시 결과값 해석으로 넘어갑시다

주성분1(comp 1)의 고유값(eigenvalue)과 분산(variance)는 각각 4.30998636, 71.8331060 입니다

주성분2(comp 2)의 고유값(eigenvalue)과 분산(variance)는 각각 1.11859590, 18.6432651 입니다

이를 시각화 해봅시다

 

 

# screeplot

klpga_pca_scree <- klpga_pca %>% fviz_screeplot()

x축은 주성분, y축은 분산비중(%)입니다

(주성분을 결과값은 comp이라고 표현하고 screeplot은 Dimension이라고 하는데 같은 말입니다

PCA() 내에서 주성분을 왜 다르게 표현하는지는 잘 모르겠습니다...;)

 

 

## 주성분(comp) 시각화하기(Biplot)

주성분을 다양한 Biplot으로 시각화하겠습니다

 

# Biplot1

klpga_pca <- klpga %>% PCA()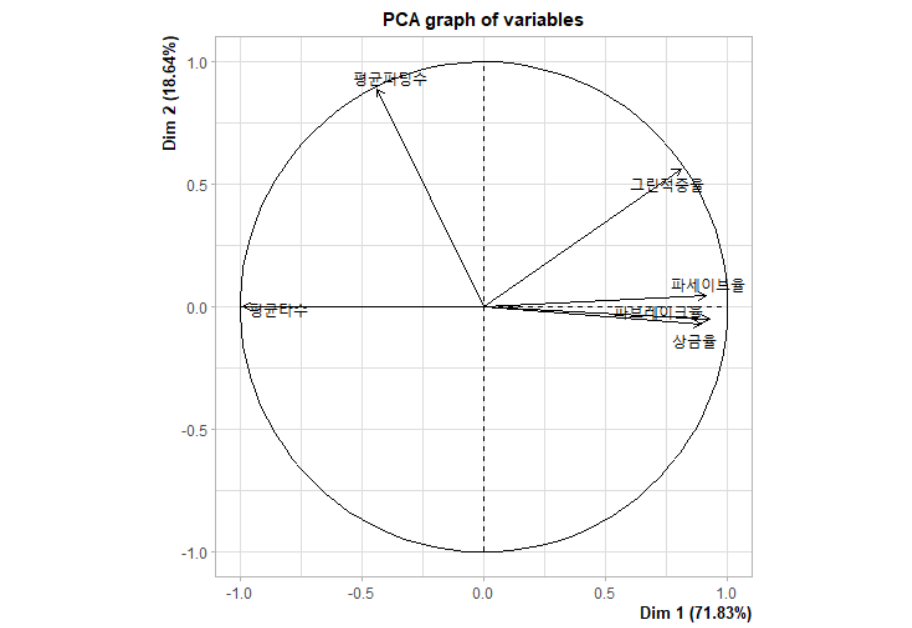

 

# Biplot2

klpga_biplot2 <- klpga_pca %>% fviz_pca_var(col.var="contrib",                                             gradient.cols = c("#a18b6b", "#002554"),                                             repel = TRUE)

# Biplot3

klpga_biplot3 <- klpga_pca %>% fviz_pca_biplot(repel = FALSE)

개인적으로는 biplot3이 가장 맘에듭니다

이상치도 어느정도 보이는군요

 

그러면 마지막 단계로 주성분의 정규성을 검정하겠습니다

 

 

## 주성분(comp) 정규성 검정

주성분 정규성은 가중치를 뽑아서 검정합니다

klpga_pca_coord <- klpga_pca$var$coord klpga_pca_coord %>% View()

 

뽑아낸 주성분 가중치를 데이터 프레임으로 만들고

주성분 1, 주성분 2에 각각에 정규성 검정(shapiro-wilk test)을 합니다

klpga_pca_coord_df <- klpga_pca_coord %>% data.frame() klpga_pca_coord_Dim1 <- klpga_pca_coord_df$Dim.1 klpga_pca_coord_Dim2 <- klpga_pca_coord_df$Dim.2 klpga_pca_coord_Dim1 %>% shapiro.test() klpga_pca_coord_Dim2 %>% shapiro.test()

주성분 1은 정규성을 만족합니다

 

주성분 2는 아슬하지만 정규성을 만족합니다

 

 

 

다음에는 범주형 변수를 포함한 데이터로 다변량 분석을 해보겠습니다

(군집 산점도, 공분산행렬 동질성)